Five Awesome Randomized Designs for Your Next Research Project

Whether you are assessing the effect of a new fertilizer on crop yields, the safety of a new drug, the influence of a teaching intervention on test scores, or the effect of smart home technology on electricity consumption, randomized experiments are the best way to prove that your idea works. Researchers often shy away from randomized experiments. Designing the experiment can seem complicated. It may be unclear why randomization is even needed. When the experiments involve humans or animals - it can be difficult to get ethical approval. In this post, I will present five simple randomized designs that you can follow for your next project and explain why using randomization is so important. Following one of these designs can make creating an experiment a snap.

Imagine that I am an engineer working for a small company that has designed a new smart home technology. I am convinced that my new technology will lead to significant savings in heating and electricity costs for homeowners. However, I need compelling evidence that my technology works. Obviously, this is not easy to prove. Heating and electricity costs vary substantially between households. And there are a huge number of confounding factors: size of the house, type of insulation used, and habits of the family living there. How can I sort out the signal from the noise? This is exactly where randomized experiments shine. Using a correctly designed randomized experiment will allow me to control for all the confounding factors and prove causality - that the use of my new technology will lead to a decrease in heating and electricity costs. Follow along as I demonstrate how each of the five randomized designs can be used to assess my new smart home technology.

1. Parallel Groups

In a parallel groups experiment, two groups are compared simultaneously. Participants are randomly assigned to one group or the other. Often, this compares a treatment group against a control group. Note that in the case of studies that involve humans it is customary to call these trials rather than experiments - probably to avoid scaring the patients.

These are the easiest randomized designs to implement. And, like all randomized designs, allow you to assess for causality, not just correlation. Analysis can also be simple, often using straightforward statistical techniques such as the t-test or proportion test.

To study my smart home technology, I could set up a simple parallel groups experiment. First, I would recruit a number of homeowners who would be willing to take part in the experiment. Then, I would randomly assign each homeowner to one of two groups by flipping a coin - heads for the treatment group and tails for the control group. The treatment group would receive the smart technology. The control group would continue using their usual solutions. I then simply compare the heating and electrical costs between the treatment and control group.

As a statistician, I have seen that where this design is most likely to go wrong is in the randomization procedure itself. Which is sad because it is so easily avoided. In a previous blog post I discussed Four Randomization Traps All Researchers Must Avoid and detailed how to properly randomize. It's important to remember that use of the word "randomized" requires the investigators to actively randomize the participants. Poor randomization can lead to invalid results. Furthermore, for published academic studies, when the randomization procedure is inadequate reviewers may insist that your study not be classified as a randomized experiment. It is not sufficient to use preexisting conditions such as ID number, name, address, or date of birth as a method of allocation. If in doubt, contact your statistician before doing the randomization. For instance, in my smart home experiment, assigning one side of the street to smart home technology and the other to standard wiring would not be a randomization as it may introduce unexpected biases: perhaps one side of the street receives more sun or is better protected from the wind. Using a coin toss, random number generator, or an online randomization tool would all be adequate.

2. Multi Arm Parallel Groups

Multi arm parallel group trials are similar to parallel group trials except they contain three or more groups. In general planning and execution is similar, although the statistical analysis is more involved as it must include correction for multiple hypotheses.

The advantage to this design is that it allows the researcher to investigate more than one treatment strategy at a time. For instance, these trials are often used to investigate dose response by trialing several doses of a medication at the same time to see which is most effective.

In the case of my smart home technology, I may decide to randomize participants into three groups. Group A could be the control group: homeowners would be asked to continue using their usual electricity and heating. Group B could be given the introductory smart home technology of Wi-Fi controlled lighting. Group C could be given the complete package of lighting and heating technology, In this way, I would be able to study the two packages in a single experiment.

The disadvantage of this design is that investigating multiple treatment strategies leads to an increased risk of committing a type-1 error: concluding a treatment strategy is effective when in fact it is not. The often used procedure of repeated t-tests or proportion tests to analyze multi arm parallel group trials is not statistically sound. Analysis must include statistical methods designed for comparing multiple groups, such as ANOVA, or include some type of correction for multiple hypothesis testing such as the Bonferroni correction.

3. Crossover

Crossover designs ensure that each participant is exposed to each treatment. Most trials of this type involve two treatments. Participants are randomized into two groups. One group starts with treatment A and then moves to treatment B. The other group starts with treatment B and then moves to treatment A. Depending on the nature of the treatment, participants may need a washout period between treatments to ensure that the effects of the treatment are worn off before the next treatment is started.

The advantage of crossover trials is that each participant serves as their own control. This can be helpful to reduce the variation among the participants.

A crossover design for my smart home experiment might work as follows. Participants are randomized to two groups. Group A uses their regular habits for 3 months, and then uses my smart home technology for three months. Group B uses the smart home technology for 3 months, and then the technology is turned off and they resume their usual habits. Analysis would then compare the heating and electrical costs for the period with smart home technology and the period without.

Analysis of crossover trials is more complicated however. Aside from comparing the differences between the periods with and without the treatment, analysis should assess to see if the order that the treatments were given has an effect. In addition, for any treatment that has a lasting effect (such as a drug or educational intervention) a washout period between the two treatments is required. For instance, it may turn out in our smart home experiment that homeowners become much more conscientious of their lighting and heating habits after using the smart home technology for several months. Although this is not fatal to the experiment, it must be analyzed appropriately to minimize false conclusions.

4. Cluster

In cluster randomized trials, participants are randomized as a group rather than an individual. The unit of randomization is often a pre-established group such as a clinic, town, school, or hospital.

This type of study is useful when it is impossible or highly impractical to randomize each individual participant.

Imagine for instance that I have approached several home builders about my smart home technology experiment. The home builders are unwilling to take part in the experiment because it is too complicated for their electricians to go from house-to-house putting in different electrical wiring. Using a cluster randomization for the smart home technology experiment may proceed as follows. I contact all the major home builders in the city asking them to participate in my study. Each home builder is randomized to either smart technology or not. For each home builder they build all their houses the same, either with the smart home technology or without depending on the randomization. At the end of the trial period I assess the heating and electrical costs of each home and analyze the correlation between my smart technology and the costs.

Caution must be used in these studies to ensure that important covariates are not introduced by the study design. Strict randomization must be adhered to and adequate sample size is needed. Perhaps in the smart home experiment we are unaware that insulation of the houses varies widely between home builders. This introduces a new bias that we were not expecting. If we have a large sample size - maybe 60 builders - then proper randomization would mitigate this bias by ensuring that on average the type of insulation between the 30 builders assigned to the smart home group and the 30 builders assigned to the control group is about the same. With small sample sizes there is the risk that all the poorly insulated homes end up in one group and our results are skewed. In my experience as a statistician, this is also one of the designs most likely to fall victim to friendomization - considering your group of friends as a random sample. For instance, perhaps I know several home builders in my city very well, and I like to work with them. Perhaps I offer these builders the opportunity to install my smart home technology, and then compare them to the other builders who do not. This is not randomization. Unless you choose your acquaintances using a random number generator - which I assume is unlikely - your friends, co-workers, or business contacts, are a very biased subgroup. People you know are more likely to follow your same ideals, values, and goals than those that you don't.

5. Factorial

Randomized factorial designs assign participants to a certain combination of treatments. This allows the investigators to study the effect of several treatments in one experiment. In a recent YouTube video we explain the benefits of factorial designs over traditional OFAT (One Factor at a Time) experiments.

Of all the randomized designs, factorial designs have the best potential to explore different factors at the same time. They are exceptionally useful for initial screening studies where investigators wish to study several potential treatments and their interactions simultaneously - often as a preface to a more dedicated parallel groups trial.

In the case of my smart home technology, a factorial design could be very effective in analyzing several different components of the technology at the same time. For instance, I could randomize participants into four groups:

1. Standard heating and lighting
2. Smart home lighting with standard heating
3. Standard lighting with smart home heating
4. Smart home lighting and heating

In addition to assessing the effect of heating and lighting individually, this experimental design also allows me to assess the interaction between the two. Does having smart home lighting also increase the effectiveness of the smart home heating? Only factorial designs give us the ability to assess the interactions.

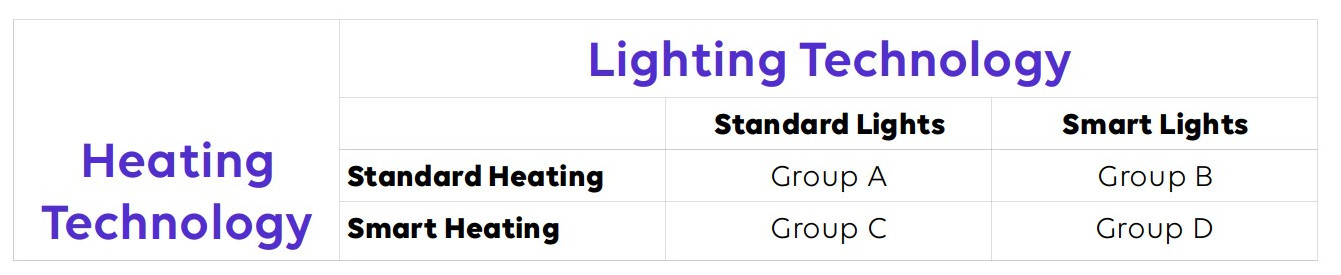
Unfortunately, there are several complications involved in factorial designs. Setting up a factorial experiment does require specialized statistical knowledge to ensure that the design is orthogonal and that interaction terms do not become hidden from analysis. Analysis is also more complicated. Finally, as most scientists are far more comfortable with OFAT designs, it can be difficult to convince ethical boards, peer reviewers, and the target audience about the validity of the method.

Picking the Right Design

Picking the right design can be tricky. By far the easiest way to structure a randomized trial is to pick one of the five study designs above and fit it to your research. In my experience, researchers who develop their own unique randomized designs waste hours of valuable time and often experience painful complications in the analysis and reporting phase. If you are creating something outside the designs above, be sure to plan your statistical analysis carefully before starting the trial to ensure that mistakes in study design do not lead to data that cannot be analyzed.

How can you maximize your likelihood of getting everyone onboard including your coworkers, co-investigators, participants, and the ethics review board? I suggest following one of the well-documented designs above and naming it in your study protocol. For instance, writing explicitly "the study will be a randomized crossover trial of two treatments" will go a long way to providing clarity for anyone who reads the protocol.

Do you want a quick visual recap of how to design a randomized experiment? Get our Five Awesome Randomized Designs infographic.